ELG-7187C – Assigment 3 (2013) - Solutions
Question 2 (20 points): Component designs from a global state machine model
This is an exercise in relation with protocol derivation from service specification. The specification formalism of Labelled Transition Systems (LTS) is to be used. The service is a simple telephone conversation. Note that the abbreviations written in italics in the following description represent local service primitives at the side of user A or user B.
Service specification: User A invites (inv) user B for a telephone conversation. Then user B accepts (acc) the call. Then this fact is acknowledged (ack) by A, and both users start talking concurrently. Talking is a sequence of talk (t) operations (we ignore the listening here!). Talking is interrupted when user A terminates (term) the call. Then user B willaccept the termination (acc-t). At the end, the system goes back to the initial state.
Your Tasks:
- Formalize the service description using the LTS notation, possibly with a hierarchical state that contains concurrent activities.
- Verify that all assumptions made for the protocol derivation discussed in class are met by your service specification. If not, try to modify your specification.
- Use the method for protocol derivation from LTS service specifications discussed in class to obtain the design of the two telephone components for user A and user B.
- Consider the following extension to the service specification: The result of inviting B is the fact that B is busy, and the service specification goes back to the initial state. Do the three steps 1, 2 and 3 again.
- Consider the original service specification with the following extension: User B may also take the initiative to terminate the call. Do the three steps 1, 2 and 3 again.
Here is a possible solution.
Question 2 (20 points): Component designs from a global Petri net behavior
The figure below shows a Petri net which defines a global behavior where the different transitions of the Petri net are performed by three different components, named 1, 2 and 3. Notation: A transition labeled Xy means that the action X associated with this transition is performed by component y.
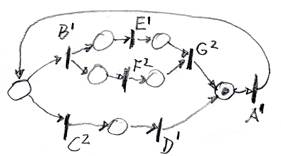
Your task is to write down three Petri nets that represent the local behavior of the three components. These Petri nets should include the actions shown in the global diagram above and transitions that correspond to the sending and receiving of coordination messages. It is suggested to use the notation “Sx(z)” and “Ry(z)” for these transitions, where “Sx(z)” means send message z to component x, and “Ry(z)” means receive message z from component y.
Here is a possible solution. But I would take another approach. By using the approach shown in this possible solution, several students had the difficulty that component 2, in the case that that alternative of transition B was chosen by component 1, had to receive two messages in parallel. Using an additional transition in component 2 to introduce this concurrency is not a good idea, because component does not know when to executed this additional transition. In the possible solution, an ad hoc modification to the component 2 was made to obtain a correct behavior. However, it is much easier, and following the derivation algorithm in a straightforward manner, by following the approach discussed in class (see slide 36 in the Powerpoint slides): (a) put the Petri net into swim lanes as shown by one student as shown here, then (b) cut the global Petri net into two parts (a sending transition has no output token, and a receiving transition does not need any input token (always enabled)) as shown here. This is the solution.
Question 3 (20 points): Derivation of component behaviors from a global specification of collaborations
Annex A is an extract from my paper Deriving Component Designs from Global Requirements, which we discussed in class. Please apply the described method to the following example:
C = ( ( C1 ;w C3 ) [] ( C2 ;s C3 ) ) ;w C4
where the behavior of the sub-collaborations C1 through C4 are defined by the diagrams below.
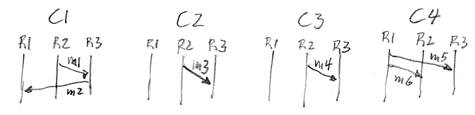
(a) What are the starting roles and terminating roles of C1 , C2, C3 and C4 ?
(b) What are the starting roles and terminating roles of ( C1 ;w C3 ) and of ( C2 ;s C3 ) ?
(c) What are the starting roles and terminating roles of C ?
(d) Can the derivation algorithm of Table 3 be applied to this example ? – (Explain what conditions must be checked).
(e) If applicable, what kind of coordination messages would the algorithm of Table 3 introduce in this example ?
(f) If applicable, give a specification of the resulting component behaviors using an FSM formalism where the transitions would be of the form “Sx(z)” or “Ry(z)” where “Sx(z)” means send message z to component x, and “Ry(z)” means receive message z from component y. These messages z may be the messages m1 through m6 mentioned in the behavior of the sub-collaborations, or these message may be coordination message described in the Annex.
Note that one needs on cim message from component 2 (that makes the choice) to component 1 which is not involved in the second alternative. One also needs a flow message for the strong order in the second alternative from component 3 to component 2 to indicate that C2 has completed.
Here is a possible solution. This solution has in part (f) the problem that one does not know in which order different messages will arrive because their order is not defined. In this possible solution, all possible orders are explicitly foreseen which leads to a very complex model for the components 2 and 3. Using the hierarchical state notation of UML with concurrent sections would lead to a more simple description of these possibilities.
However, what I proposed in my paper (and also discussed in class) is to assume that each component has a message pool, and the behavior model of the component will determine which are the possile next messagse that could be consumed (and wait for one of them, if none is not in the message pool). This approach leads to a much simpler behavior model as shown here.
Note: Here is a short explanation of the meaning of Alloc(R) which occurs in the tables in the annex of Assignment 3.
In the paper from which these tables are taken, one makes a distinction between the different system components and the different roles that define the different parties involved in the behavior description of the collaborations. The roles in the behavior descriptions represent some logical entities in the environment that are involved in the execution of the collaborations, but no assumptions are made on how these roles are implemented. It is assumed that each of the different system components implements a certain subset of roles. Each system component also contains a protocol entity that performs the local actions of the locally implemented roles and the exchange of messages with the other protocol entities on the other system components which are necessary for coordinating the global order of execution of these actions.
Alloc(r) is a function that has as result the system component that implements the role r. In the table, I often use the function Alloc(R) which returns for a given set of roles R, the set of system components that are involved in the implementation of these roles.
Annex A
Table 1: Operators used in behavior expressions
Construct |
Notation |
Explanation of the semantics |
primitive activity |
<action>(r) |
Execution of a local action with name <action> performed by role r |
invocation of sub-col. |
<subcol>(R) |
Execution of a collaboration with name <subcol> involving the set R of participating roles |
strong sequence |
C1 ;s C2 |
C2 is executed after C1 in strong sequence, that is, all actions of C1 are completed before C2 can start |
weak sequence |
C1 ;w C2 |
C2 is executed after C1 in weak sequence, that is, only local order is enforced by each participating role |
choice |
C1 [] C2 |
Either C1 or C2 is executed; this may be a local choice (that is, the choice is performed by a single role / component) or competing initiatives from several roles; for a more detailed discussion, see [2]) |
strong while loop |
C1 * s C2 |
C1 is executed zero, one or more times and then C2 will be executed; more precisely, the behavior starts with a choice between C1 and C2 ; if C1 is executed, there is strong sequencing between the end of C1 and the choice of executing C1 again or terminating the loop with C2 ; we assume that the choice is local (performed by a single role). |
weak while loop |
C1 * w C2 |
As above, except that weak sequencing is used between the end of C1 and the choice of executing C1 again or terminating the loop with C2 |
concurrency |
C1 || C2 |
C1 and C2 are executed concurrently |
interruption |
C1 |> C2 else C3 |
C1 is executed, but may be interrupted by C2 which represents a choice with priority; C2 is enabled as soon as C1 starts. If C2 does not occur (or occurs when C1 is already terminated) then C3 will occur after C1 (this is the other choice alternative). |
Table 2: Rules for calculating the starting, terminating and participating roles
Operator |
Starting roles (SR) |
Terminating roles (TR) |
Participating roles (PR) |
<action>(r) |
{r} |
{r} |
{r} |
<subcol>(R) |
SR(<name>) |
TR(<name>) |
PR(<name>) = R |
C1 ;s C2 |
SR(C1) |
TR(C2) |
PR(C1) U PR(C2) |
C1 ;w C2 |
SR(C1) U
(SR(C2) - PR(C1)) |
TR(C2) U
(TR(C1) - PR(C2)) |
PR(C1) U PR(C2) |
C1 [] C2 |
SR(C1) U SR(C2) |
TR(C1) U TR(C2) |
PR(C1) U PR(C2) |
C1 * s C2 |
SR(C1) = SR(C2)= {r} |
TR(C2); SR(C1) if C2= ε |
PR(C1) U PR(C2) |
C1 * w C2 |
as above |
TR(C2) U
(TR(C1) - PR(C2)) |
PR(C1) U PR(C2) |
C1 || C2 |
SR(C1) U SR(C2) |
TR(C1) U TR(C2) |
PR(C1) U PR(C2) |
C1 |> C2 else C3 |
SR(C1) |
TR(C2) U TR(C3) |
PR(C1) U PR(C2) U PR(C3) |
Table 3: Required coordination messages
Construct |
Notation |
Required coordination messages |
Primitive act |
<action>(r) |
The action is included in the behavior of the component Alloc(r). - No message. |
invocation of
a sub-collab. |
subcol(R) |
The invocation is included in the behaviors of the components in Alloc(R).
- No message required. |
strong sequence |
C1 ;s C2 |
A flow message is sent by each component in Alloc(TR(C1)) (when the execution of C1 is completed) to all components in Alloc(SR(C2)); these components will receive these flow messages before starting the execution of C2. This was already described in [3, 4, 5]. We note that in the case that C1 contains alternatives, the set Alloc(TR(C1)) may be larger than necessary (see note in Table 2). Therefore we may introduce more flow messages than necessary. The approach described in [3, 4] avoids such unnecessary messages. |
weak sequ. |
C1 ;w C2 |
No coordination messages required. |
choice |
C1 [] C2 |
(a) If the choice is not local, that is, if Alloc(SR(C1) U SR(C2)) contains more than one component, then coordination messages for organizing the choice are required.
(b) If a component is in Alloc(PR(C1)) but not in Alloc(PR(C2)), then the component should receive a message from one of the components in Alloc(PR(C2)) when choice C2 is performed (this is a choice indication message). The component may then enable the sub-collaboration that follows the choice. |
strong while loop |
C1 * s C2 |
(a) If a component is in Alloc(PR(C1)) but not in Alloc(PR(C2)) and is not the starting component of C1, then it should receive a message from the latter when C2 is performed (this is a choice indication message) or from one of the components in Alloc(PR(C2)). (We note that this is not required if the component has no starting role for the collaboration(s) that follow the strong while loop, because it would be invited for following collaboration by a message).
(b) As in the case of strong sequencing, there are flow messages sent, when C1 ends, from the components in Alloc(TR(C1)) to the component starting C1. |
weak while loop |
C1 * w C2 |
As above, however, the flow messages under (b) are not required. In addition, if a component is in Alloc(PR(C1)) and in Alloc(PR(C2)), then the message starting the execution of C2 in this component should contain a counter indicating the number of times C1 was executed. The same parameter should be included in the choice indication messages under (a). Note: this allows delaying the consumption of this message until a sufficient number of messages concerning C1 have already been consumed; this avoids the problem shown in Figure 9(c) of [1]. |
concurrency |
C1 || C2 |
No coordination messages required. |
interruption |
C1 |> C2 else C3 |
(a) We assume that C2 has a single starting role,
and is of the form “ <action>(r) ;s C2’ “.
(b) When a starting role of C1 starts the execution of C1, it sends an interrupt enable message to the starting role of C2; when such a message is received, C2 becomes enabled.
(c) When the interrupt action <action>(r) occurs, the component performing role r will send interrupt messages to all components in Alloc(PR(C1)); when these components receive this message, they will know that an interrupt occurred. If they have not yet completed the execution of C1 they will be in the “interrupted” state.
(b) Flow messages will be sent by all components in Alloc(PR(C1)) to all starting components of C’2 and C3. These messages include a Boolean parameter indicating whether the component was “interrupted”. The starting components of C’2 and C3, when they have received these messages, will know whether C’2 or C3 should be executed (C3 will be executed only if no component was “interrupted”). |

